Méthodologie¶

À l’année de départ, la base de données de simulation de SimGen correspond à la Base de données de simulation de politiques sociales (BDSPS) de 2017 de Statistique Canada. Cette base de données est composée d’observations statistiquement représentatives des particuliers canadiens et québécois dans leur contexte familial.

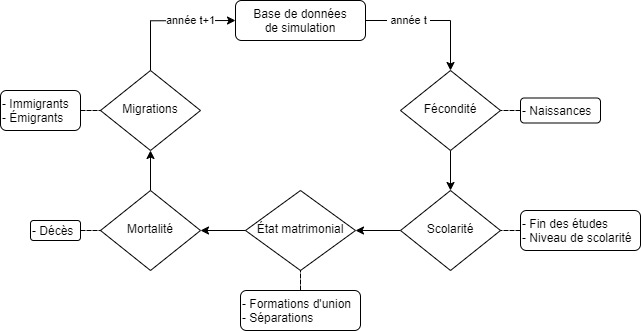
Durant les année ultérieures, SimGen fait évoluer chaque individu selon les transitions suivantes dans l’ordre suivant:

Fécondité
Scolarité
État matrimonial
Mortalité
Migrations

De nouvelles observations sont ajoutées dans la base de données de simulation lors des transitions de fécondité (naissances) et d’immigration. À l’opposé, certaines observations sont retirées de la base de données lors des transitions de mortalité (décès) et d’émigration. La figure suivante illustre plus explicitement la dynamique des transitions:

Lorsque SimGen arrive à l’année de fin de la simulation, celui-ci recommence le processus de simulation de l’année de départ à l’année de fin, jusqu’à ce que le nombre de réplications sélectionné soit atteint. Une fois cette étape accomplie, la moyenne des résultats des réplications est calculée afin de créer la base de données finale des résultats.

Structure des données

De manière plus spécifique, la base de données de simulation de SimGen est composée de trois registres. Un premier registre contient les individus dominants, un deuxième contient les conjoints de ceux-ci et un troisième contient leurs enfants. Le registre des individus dominants représente l’échantillon principal sur lequel les transitions sont appliquées et sur lequel les sorties statistiques sont basées. Les registres des conjoints et des enfants servent essentiellement à décrire le contexte familial des individus dominants. Ils ne sont donc pas inclus dans les sorties statistiques. Cette approche a été choisie car elle permet de simplifier le processus de simulation et de rendre plus flexible la production de résultats (voir le document suivant de Statistique Canada pour des explications sur les différentes approches possibles des modèles de microsimulation).

Fécondité¶

Modèle économétrique¶

Pour chaque rang de naissance d’un enfant (k=1,2,3), la probabilité d’avoir un enfant est estimée à l’aide d’un modèle logistique incluant trois groupes de variables explicatives liées à l’âge, au niveau de scolarité et à l’âge du dernier enfant, le cas échéant.

\[\mu_{i,t,k} = \mu_{0,k} + \mu_{1,k} age_{i,t} + \mu_{2,k} edu_{i,t} + \mu_{3,k} lkidage_{i,t}\]

\[\Pr(b_{i,t}=1) = \frac{\exp(\mu_{i,t,k})}{1+\exp(\mu_{i,t,k})}\]

Données et échantillon¶

Les effets marginaux sont calculés à partir des vagues 2006 et 2011 de l’Enquête sociale générale (ESG) menée auprès des ménages par Statistique Canada.

L’échantillon utilisé pour calculer les 3 régressions logistiques des transitions de naissance est défini en suivant plusieurs étapes:

Les données des vagues 2006 et 2011 de l’ESG sont regroupées dans une base unique.

L’échantillon est ensuite restreint aux données du Québec (variable prv).

Un fichier de pseudo panel des répondants qui recense l’historique des transitions de naissances 1, 2 et 3 est créé (calcul des naissances pour chaque année à partir des variables agechdc1, agechdc2 et agechdc3 correspondant à l’âge des enfants d’ordre 1, 2 et 3).

Seul l’historique des transitions du pseudo panel depuis 30 années est conservé afin d’éviter les effets des cohortes les plus anciennes (1976 à 2006 pour l’ESG de 2006 et 1981 à 2011 pour celle de 2011).

L’échantillon est finalement restreint aux femmes âgées de 18 à 44 ans inclusivement.

Variables du modèle¶

Les variables dépendantes pour les régressions 1, 2 et 3 sont des variables indicatrices, égales à 1 lors de l’année de naissance de l’enfant d’ordre k=1,2,3 et égales à 0 depuis l’année de naissance du dernier enfant (pour les naissances d’ordre 2 et 3) ou depuis 18 ans pour le premier enfant (naissance d’ordre 1).

Prenons l’exemple d’une femme qui a eu deux enfants : un enfant à 20 ans et un enfant à 30 ans. Dans ce cas, la variable dépendante pour le premier enfant sera égale à 0 de 18 ans à 19 ans, puis elle sera égale à 1 à 20 ans. La variable dépendante pour le second enfant sera égale à 0 de 21 ans à 29 ans et elle sera égale à 1 à l’âge de 30 ans.

Variables explicatives d’âge (variables indicatrices):

age1824 (référence): la femme a entre 18 et 24 ans.

age2529: la femme a entre 25 et 29 ans.

age3034: la femme a entre 30 et 34 ans.

age3539: la femme a entre 35 et 39 ans.

age40p: la femme a entre 40 et 44 ans.

Variables explicatives d’éducation (variables indicatrices, notées « edu » dans l’équation du modèle économétrique):

insch: la femme n’a pas terminé ses études.

inf (référence): la femme a terminé ses études, mais n’a pas complété ses études secondaires.

des: la femme a terminé ses études et a un diplôme d’études secondaires ou des études partielles à l’université ou au cégep.

dec: la femme a terminé ses études et a un diplôme d’études collégiales.

uni: la femme a terminé ses études et a un diplôme égal ou supérieur au baccalauréat.

Variable du dernier enfant:

lkidage: âge du dernier enfant né. Cette variable est uniquement utilisée pour les naissances d’ordre 2 et 3.

Résultats de régression¶

Les résultats des régressions logistiques sont présentés dans le tableau suivant:

Logit - Coefficients des transitions de naissances¶
Variables	1er enfant	2e enfant	3e enfant
age2529	.5111452	.20215	-.1745108
age3034	.0206863	.0036399	-.7896601
age3539	-.8569678	-.8245546	-1.621034
age40p	-1.939295	-2.335598	-3.388722
insch	-1.025785	.1545281	.4842334
des	-.223628	.1972002	.0498862
dec	-.1165148	.1987852	.2902924
uni	-.1596642	.4500001	.8004084
lkidage	0	-.0990092	-.0377307
constant	-2.532843	-1.634364	-2.288871

Mise en œuvre¶

La mise en œuvre dans SimGen est réalisée par un tirage uniforme, indépendant par individu dominant. Une naissance survient lorsque le résultat de ce tirage est inférieur à la probabilité logistique prédite. Dans SimGen, les personnes à risque pour cette transition sont les femmes en couple (qu’elles soient enregistrées comme individu dominant ou conjointe) âgées de 18 à 44 ans inclusivement.

Scolarité¶

Tous les enfants débutent leurs études l’année de leurs 5 ans. La présente transition calcule la probabilité qu’un individu finisse ses études. S’il est déterminé que cet individu termine ses études durant l’année en cours, un niveau de scolarité lui est ensuite attribué.

Modèle économétrique¶

Deux régressions logistiques sont réalisées pour 1) calculer la probabilité de finir ses études; 2) attribuer un niveau de scolarité aux individus qui ont complété leurs études. Une régression logistique dichotomique est appliquée pour calculer la probabilité de finir ses études et un modèle logistique multinomial est utilisé afin d’attribuer le niveau de scolarité correspondant.

probabilité dpour un individu i de finir ses études (f = 1) à l’année t:

\[\mu_{i,t} = \mu_{0} + \mu_{1} age_{i,t} + \mu_{2} male_{i,t} + \mu_{3} father_{i,t} + \mu_{4} mother_{i,t}\]

\[\Pr(f_{i,t}=1) = \frac{\exp(\mu_{i,t})}{1+\exp(\mu_{i,t})}\]

pour chaque niveau de scolarité e = 1 (n’a pas terminé ses études secondaires), 2 (diplôme d’études secondaires) [référence], 3 (diplôme d’études collégiales), 4 (diplôme égal ou supérieur au baccalauréat) atteint par un individu i l’année de terminaison des études en t:

\[\mu_{e(i,t)} = \mu_{0} + \mu_{i} age_{i,t} + \mu_{j} male_{i,t} + \mu_{k} father_{i,t} + \mu_{l} mother_{i,t}\]

\[\Pr(e_{i,t}=1) = \frac{\exp(\mu_{1(i,t)})}{1+\exp(\mu_{1(i,t)})+\exp(\mu_{3(i,t)})+\exp(\mu_{4(i,t)})}\]

\[\Pr(e_{i,t}=2) = \frac{1}{1+\exp(\mu_{1(i,t)})+\exp(\mu_{3(i,t)})+\exp(\mu_{4(i,t)})}\]

\[\Pr(e_{i,t}=3) = \frac{\exp(\mu_{3(i,t)})}{1+\exp(\mu_{1(i,t)})+\exp(\mu_{3(i,t)})+\exp(\mu_{4(i,t)})}\]

\[\Pr(e_{i,t}=4) = \frac{\exp(\mu_{4(i,t)})}{1+\exp(\mu_{1(i,t)})+\exp(\mu_{3(i,t)})+\exp(\mu_{4(i,t)})}\]

Données et échantillon¶

Les régressions logistiques sont réalisées à l’aide des vagues 2006 et 2011 de l’Enquête sociale générale (ESG) menée auprès des ménages par Statistique Canada.

L’échantillon utilisé pour calculer les transitions de scolarité est défini en suivant plusieurs étapes:

Les données des vagues 2006 et 2011 de l’ESG sont regroupées (pooled) dans une base unique.

L’échantillon est restreint aux données du Québec (variable prv).

Un fichier de pseudo panel des répondants qui recense l’historique des transitions de fin d’études et le niveau de scolarité associé est créé.

Seul l’historique des transitions du pseudo panel depuis 30 années est conservé afin d’éviter les effets des cohortes les plus anciennes (1976 à 2006 pour l’ESG de 2006 et 1981 à 2011 pour celle de 2011).

L’échantillon est restreint aux individus âgés de 17 à 35 ans inclusivement.

Les années qui suivent l’année de terminaison des études sont supprimées.

Pour la régression logistique multinomiale du niveau de scolarité, l’échantillon est restreint à l’année de terminaison des études.

Variables du modèle¶

La variable dépendante schldone définissant la probabilité de finir ses études est égale à 1 lorsque l’individu a terminé ses études, et elle est égale à 0 lorsque l’individu n’a pas encore terminé ses études. Cette variable indicatrice est calculée à partir de la variable agecmplt (âge du répondant à la fin des études) de l’ESG.

La variable dépendante et indicatrice du niveau de scolarité, « educ », est utilisée dans une régression logistique multinomiale. Elle inclut 4 niveaux de scolarité:

inf: n’a pas terminé ses études secondaires.

des (référence): a obtenu un diplôme d’études secondaires ou des études partielles à l’université ou au cégep.

dec: a obtenu un diplôme d’études collégiales.

uni: a obtenu un diplôme égal ou supérieur au baccalauréat.

Les variables explicatives et indicatrices de la fin des études, « schldone », et du niveau de scolarité atteint sont les suivantes:

male: égal à 1 si le répondant est un homme et égal à 0 si le répondant est une femme.

father: égal à 1 si le répondant est un homme avec des enfants, 0 sinon.

mother: égal à 1 si le répondant est une femme avec des enfants, 0 sinon.

agex: égal à 1 si l’individu a x ans, 0 sinon, avec x = 17 à 35 ans (la catégorie de référence est constituée des individus âgés de 17 ans).

Résultats de régression¶

Les résultats des régressions logistiques sont présentés dans le tableau suivant:

Logit - Coefficients de la transition de fin d’études (colonne 2) et d’attribution du niveau de scolarité (colonne 3 à 5)¶
Variables	Fin etudes	Inf. secondaire	Collegial	Universitaire
male	.18436	.410925	-.190319	-.598743
mother	-.184402	.317556	.170107	-1.0691
father	-.182383	-.609737	-.423941	-.688694
age18	-.108408	2.5816	2.69061	1.86966
age19	.376351	2.18569	3.05998	2.89381
age20	.832675	-35.5138	3.13082	4.12123
age21	.849631	-34.2392	3.51179	5.73524
age22	1.13566	-33.5076	3.37148	6.74679
age23	1.33625	-34.0375	2.75714	6.94923
age24	1.23258	-17.3182	2.7163	7.07475
age25	1.08433	-17.6177	2.45016	6.60651
age26	.960907	-17.5423	2.60372	6.72941
age27	1.06736	-17.2421	3.01988	6.7807
age28	1.02315	-17.1569	3.16667	6.96461
age29	1.00341	-17.3664	2.61141	7.11651
age30	.875271	-17.8062	2.1641	6.38981
age31	.994532	-17.6105	2.34907	6.83184
age32	1.36367	-17.3727	2.69095	6.95154
age33	1.52	-16.9129	3.37866	7.38962
age34	1.95557	-1.56612	2.70337	6.27352
age35	2.4045	-2.35543	2.26993	6.41581
constant	-3.1736	-.133584	-1.66927	-5.01949

Mise en œuvre¶

La mise en œuvre dans SimGen est réalisée à l’aide d’un tirage uniforme, indépendant par individu dominant, et la fin des études et le niveau de scolarité associé sont déterminés lorsque le résultat de ce tirage est inférieur à la probabilité logistique prédite.

Dans SimGen, les personnes à risque pour cette transition sont les individus dominants âgés de 17 à 35 ans qui sont encore aux études. Les individus âgés de 35 ans ont une probabilité de terminer leurs études fixée à 100%. Avant l’année de fin des études, les individus sont considérés sans scolarité (aucun niveau ne leur est attribué). Le niveau de scolarité obtenu l’année de fin des études est attribué aux individus jusqu’à la fin de leur vie. Aucun retour aux études n’est possible après la fin des études.

État matrimonial¶

Modèle économétrique¶

Deux régressions logistiques sont réalisées pour 1) calculer la probabilité d’entrer dans une union conjugale (union libre ou mariage, indistinctement); 2) calculer la probabilité de se séparer. La probabilité d’entrer en union et de se séparer dépend de variables similaires liées à l’âge du répondant, à son genre et à son niveau de scolarité. De plus, la probabilité de se séparer dépend également de la présence d’au moins un enfant âgé de moins de 18 ans.

probabilité c pour un individu i de se mettre en couple l’année t:

\[\mu_{i,t} = \mu_{0} + \mu_{1} age_{i,t} + \mu_{2} male_{i,t} + \mu_{3} educ_{i,t}\]

\[\Pr(c_{i,t}=1) = \frac{\exp(\mu_{i,t})}{1+\exp(\mu_{i,t})}\]

probabilité s pour un individu i de se séparer l’année t:

\[\mu_{i,t} = \mu_{0} + \mu_{1} age_{i,t} + \mu_{2} male_{i,t} + \mu_{3} educ_{i,t} + \mu_{4} kid_{i,t}\]

\[\Pr(s_{i,t}=1) = \frac{\exp(\mu_{i,t})}{1+\exp(\mu_{i,t})}\]

Données et échantillon¶

Les modèles logistiques sont estimés à partir des vagues 2006 et 2011 de l’Enquête sociale générale (ESG) réalisée auprès des ménages par Statistique Canada.

L’échantillon utilisé pour calculer les transitions matrimoniales est défini en suivant plusieurs étapes:

Les données des vagues 2006 et 2011 de l’ESG sont regroupées dans une base unique.

L’échantillon est ensuite restreint aux données de la province du Québec (variable prv).

Un fichier de pseudo panel des répondants qui recense l’historique des transitions d’unions et de séparations d’ordre 1 à 4 est créé (jusqu’à 4 unions et séparations sont donc permises tout au long de la vie).

Seul l’historique des transitions du pseudo panel depuis 30 années est conservé afin d’éviter les effets des cohortes les plus anciennes (1976 à 2006 pour l’ESG de 2006 et 1981 à 2011 pour celle de 2011).

Variables du modèle¶

Pour calculer la transition de mise en union, la variable dépendante est égale à 0 lorsque l’individu est célibataire et la variable dépendante est égale à 1 à partir de l’année de la mise en couple. Symétriquement, pour le calcul de la transition de séparation, la variable dépendante est égale à 0 lorsque l’individu est en couple et la variable dépendante est égale à 1 à partir de l’année de la séparation. Il faut préciser que le fait de devenir veuf n’est pas considéré comme une transition de séparation dans le modèle logistique.

1) Variables explicatives des transitions de mise en couple

Genre (variable indicatrice):

male: égal à 1 si le répondant est un homme et égal à 0 si le répondant est une femme.

Âge (variables indicatrices):

age1619: le répondant a entre 16 et 19 ans.

age2024: le répondant a entre 20 et 24 ans.

age2529: le répondant a entre 25 et 29 ans.

age3034 (référence): le répondant a entre 30 et 34 ans.

age3539: le répondant a entre 35 et 39 ans.

age4044: le répondant a entre 40 et 44 ans.

age4549: le répondant a entre 45 et 49 ans.

age5054: le répondant a entre 50 et 54 ans.

age5559: le répondant a entre 55 et 59 ans.

age6065: le répondant a entre 60 et 65 ans.

Scolarité (variables indicatrices):

insch: le répondant n’a pas encore terminé ses études.

inf (référence): le répondant a terminé ses études mais n’a pas complété ses études secondaires.

des: le répondant a terminé ses études et a un diplôme d’études secondaires ou des études partielles à l’université ou au cégep.

dec: le répondant a terminé ses études et a un diplôme d’études collégiales.

uni: le répondant a terminé ses études et a un diplôme égal ou supérieur au baccalauréat.

2) Variables explicatives des transitions de séparation

Genre (variable indicatrice):

male: égal à 1 si le répondant est un homme et égal à 0 si le répondant est une femme.

Âge:

mage: âge du répondant si c’est un homme, 0 sinon.

mage2: âge au carré du répondant si c’est un homme, 0 sinon.

mage3: âge au cube du répondant si c’est un homme, 0 sinon.

wage: âge du répondant si c’est une femme, 0 sinon.

wage2: âge au carré du répondant si c’est une femme, 0 sinon.

wage3: âge au cube du répondant si c’est une femme, 0 sinon.

Scolarité (variables indicatrices):

insch: le répondant n’a pas encore terminé ses études.

inf (référence): le répondant a terminé ses études mais n’a pas complété ses études secondaires.

des: le répondant a terminé ses études et a un diplôme d’études secondaires ou des études partielles à l’université ou au cégep.

dec: le répondant a terminé ses études et a un diplôme d’études collégiales.

uni: le répondant a terminé ses études et a un diplôme égal ou supérieur au baccalauréat.

Enfants (variable indicatrice):

kid: égal à 1 si le répondant a au moins un enfant de moins de 18 ans, 0 sinon.

Cette variable contrôle pour la présence d’enfants mineurs, potentiellement résidants au domicile parental ou bien à la charge de leurs parents. La présence d’enfants majeurs n’est pas prise en compte car ceux-ci ne sont potentiellement plus à la charge de leurs parents.

Résultats de régression¶

Les résultats du modèle logistique de mise en couple sont présentés dans le tableau suivant:

Logit - Coefficients des transitions de mise en couple¶
Variables	Coefficients
male	-.1837456
age1619	-.6663195
age2024	.3110995
age2529	.4030818
age3539	-.3277921
age4044	-.399524
age4549	-.5470281
age5054	-.4505239
age5559	-.8944283
age6065	-.8323357
insch	-.732394
des	.1500707
dec	.3124948
uni	.3111567
constant	-2.408129

Les résultats du modèle logistique de séparation sont présentés dans le tableau suivant:

Logit - Coefficients des transitions de séparations¶
Variables	Coefficients
male	-.7359777
mage	-.277098
mage2	.0087923
mage3	-.0000819
wage	-.327683
wage2	.0098783
wage3	-.0000913
insch	.6755069
des	-.1025277
dec	-.1902154
uni	-.4476943
kid	-.5016676
constant	.2193172

Mise en œuvre¶

La mise en œuvre des transitions de formation d’union et de séparation dans SimGen est réalisée par un tirage uniforme, indépendant par individu dominant, et ces événements surviennent lorsque le résultat de ce tirage est inférieur à la probabilité prédite.

Lorsqu’un individu dominant D1 est sélectionné pour former une union, une banque d’individus dominants est créée à partir des individus en couple, ayant les mêmes caractéristiques que ce dernier quant à l’âge, le genre et le niveau de scolarité et ayant une différence d’âge avec leur conjoint de moins de 5 ans. Si aucun individu dominant en couple avec ces caractéristiques n’est trouvé, un nouvelle banque d’individus dominants est créée à partir des individus dominants en couple, ayant les mêmes caractéristiques que l’individu dominant D1 quant au genre et au niveau de scolarité, et ayant une différence d’âge avec leur conjoint de moins de 20 ans. Par la suite, les caractéristiques du conjoint C1 de l’individu dominant D1 sont obtenues en attribuant à ce conjoint les mêmes caractéristiques que le conjoint C2 d’un individu dominant D2 sélectionné aléatoirement à partir de la banque d’individus dominants créée à cet effet.

Mortalité¶

Chaque année t, un individu d’âge a et de genre g a une probabilité P(t,a,g) de décéder. Cette probabilité, définie comme un taux de mortalité, est calculée à partir des quotients prospectifs de mortalité selon l’âge et le sexe estimés par Statistique Canada entre 2013-2014 et 2062-2063 (juillet-juin) pour les provinces et territoires. Le rapport technique de Statistique Canada présente la méthodologie et les hypothèses utilisés pour construire ces quotients prospectifs.

L’âge, le genre et la cohorte de naissance sont donc les seuls déterminants de l’espérance de vie des individus. Notons également que les immigrants et les natifs ont des probabilités équivalentes de décès en fonction de leur âge, de leur genre et de leur cohorte.

Migrations¶

Immigration¶

Le taux prospectif d’immigration internationale est égal à 6,6‰. Ce taux est calculé en divisant le nombre d’immigrants projeté dans le scénario de référence de l’ISQ (55 000) par la population québécoise enregistrée par Statistique Canada en 2017 (8 302 063). Les caractéristiques socio-économiques et démographiques des nouveaux immigrants internationaux sont attribuées en fonction des immigrants internationaux récents issus de la BDSPS de Statistique Canada pour l’année 2017. Chaque année t, on tire aléatoirement dans la base de départ 6,6 pour mille de la sous-population des immigrants récents (depuis 5 ans ou moins). Les caractéristiques socio-économiques et démographiques des nouveaux immigrants sont alors celles des immigrants tirés de la BDSPS de 2017: l’âge, le genre, le niveau de scolarité, la présence de conjoint et le nombre d’enfants.

Émigration¶

Les caractéristiques des émigrants dépendent uniquement de l’âge. L’émigration intègre les émigrants internationaux ainsi que le solde migratoire interprovincial. À chaque âge donné, la probabilité d’émigrer est égale pour toutes les personnes dominantes. Les émigrants d’un âge donné sont tirés de manière aléatoire. De plus, on considère que le(la) conjoint(e) du dominant ainsi que tous ses enfants âgés de moins de 18 ans émigrent avec la personne dominante. Le taux d’émigration par âge est calculé à partir du nombre d’émigrants interprovinciaux par classe d’âge en 2018-2019 du tableau 17-10-0015-01 « Estimations des composantes de la migration interprovinciale, par âge et sexe, annuelles », du nombre d’émigrants internationaux par classe d’âge en 2018-2019 du tableau 17-10-0014-01 « Estimations des composantes de la migration internationale, par âge et sexe, annuelles » et de la population québécoise par classe d’âge au 1er juillet 2018 du tableau 17-10-0005-01 « Estimations de la population au 1er juillet, par âge et sexe ». À noter que le nombre d’émigrants interprovinciaux à chaque âge a été normalisé sur les hypothèses du solde interprovincial annuel de l’ISQ (9 000 personnes). Les taux d’émigration par classe d’âge sont les suivants:

Classe d’âge	Taux d’émigration (‰)
15 à 19 ans	1,37
20 à 24 ans	3,08
25 à 29 ans	5,03
30 à 34 ans	4,90
35 à 39 ans	3,74
40 à 44 ans	2,72
45 à 49 ans	2,00
50 à 54 ans	1,38
55 à 59 ans	0,99
60 à 64 ans	0,84
65 à 69 ans	0,82
70 à 74 ans	0,64
75 à 79 ans	0,65
80 à 84 ans	0,62
85 à 89 ans	0,55
90 ans et plus	0,41